arctan(1.76)目录
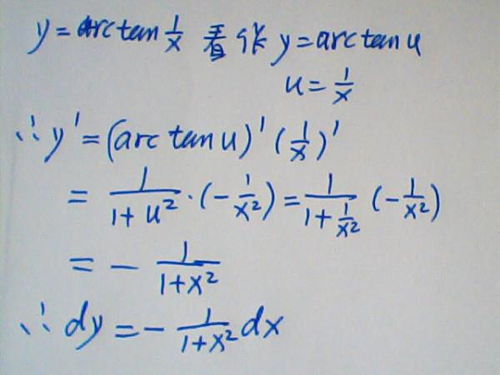
arctan(1.76)的计算和应用。
简介
。在三角学中,反正切函数(arctan)是切线函数的逆函数,用于计算已知切线值的角度。
计算arctan(1.76)
。使用计算器或数学软件,我们可以计算出arctan(1.76)的近似值:。
。$$。
arctan怎么化成tan">arctan怎么化成tan
如何将Arcta化简为Ta
前言
Arcta(反正切)函数与ta(正切)函数密切相关,在三角学和高等数学中有着广泛的应用。有时,我们需要将arcta化简为ta。本文将详细介绍如何执行此操作,包括分步说明和示例。
分步说明
要将arcta化简为ta,可以使用以下步骤:
1.应用正切恒等式:ta(arcta(x))=x。此恒等式表明arcta函数的正切值等于其输入。
2.替换arcta(x)为y:arcta(x)=y。此替换简化了方程。
3.将y代入ta(arcta(x))=x:ta(y)=x。
4.求解ta(y):y=ta^-1(x)。此步骤得到了ta(arcta(x))的逆值。
5.简化结果:ta^-1(x)=ta(x)。
示例
例如,让我们将arcta(1/2)化简为ta:
1.应用正切恒等式:ta(arcta(1/2))=1/2
2.替换arcta(1/2)为y:arcta(1/2)=y
3.将y代入ta(arcta(1/2))=1/2:ta(y)=1/2
4.求解ta(y):y=ta^-1(1/2)
5.简化结果:ta^-1(1/2)=ta(1/2)
因此,arcta(1/2)=ta(1/2)。
结论
通过遵循这些步骤,您可以轻松地将arcta化简为ta。这对于解决三角学问题和理解三角函数之间的关系至关重要。下次您需要执行此转换时,请使用本文作为参考。
arctax的特殊值表
简介
反正切函数(arctax)三角函数的逆函数,它提供了给定正切值x时与单位圆相关的角度值。此表列出了arctax的一些重要特殊值。
特殊值表
|x|arctax|
|---|---|
|0|0|
|1|π/4|
|√3/3|π/6|
|1/2|π/6|
|√3|π/3|
|1|π/4|
|∞|π/2|
|-1|-π/4|
|-√3/3|-π/6|
|-1/2|-π/6|
|-√3|-π/3|
|-1|-π/4|
|-∞|-π/2|
应用
arctax的特殊值表在以下领域非常有用:
三角恒等式求解
角的转换
复数的表示
微积分中的积分求解
结论
arctax的特殊值表是一个重要的工具,可用于快速轻松地查找特定正切值的arcta值。了解这些特殊值对于三角学及其他数学领域至关重要。
标签
arctax
三角函数
特殊值
数学 arcta负∞等于多少?
定义
arcta函数,也称为反正切函数,是正切函数的逆函数。正切函数计算以弧度表示的角度的正切值,而反正切函数计算具有给定正切值的角。
象限限制
正切函数的定义域为实数集R,值域为开区间(-∞,∞)。这表示正切函数可以取任何实数值,但不能取负无穷大或正无穷大。
反函数的定义域和值域
由于正切函数的定义域不是正负无穷大,所以其反正切函数的定义域也不是正负无穷大。
arcta(-∞)的值
与arcta(∞)一样,arcta(-∞)的值也是未定义的,因为它不属于反正切函数的定义域。
